ベクトルを学習すると必ず「内積って何なんだ!?」という疑問に直面すると思います。
ベクトルの和，差と習ってきたから，次は掛け算や割り算でも習うのかな?と思ったら「ベクトルには掛け算はない!」と言われ，「変わりにこんなのがある!」ということで突然導入されるのが内積という概念です。
感覚的には掛け算と覚えても良いのですが。。。
まずは復習ですが，２つのベクトルa→とb→の内積とは，
a→・b→=|a→| |b→|cosθ
で定義されます。θは２つのベクトルの始点をそろえたときにできる「なす角」です。
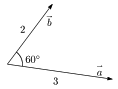
例えば右の図のような場合，a→とb→の内積は ２×３×(１/２)＝３ということになります。
しかしいったい，この「３」という数値は何を意味しているのでしょうか。
内積は「b→が，a→の方向に，a→と共に行った仕事の量である」という説明ができます。
具体例
右のような例で説明しましょう。
ゴールを目指してレースをしているヨットがあるとします。このヨットは風速1mの風で3m進むことができる性能を持っているとしましょう。
つまり，風速10mの風が吹けば，30m進むことができるわけです。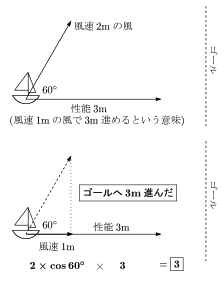
しかし，風というのは気まぐれですから，必ずしもゴールに向かって真っ直ぐ吹いてくれるとは限りませんよね。
図のように，ゴールに向かって60°の角度で，風速2mの風が吹く場合もあります。
この場合，せっかく2mの風が吹いていても，実際にゴールに進むのに役立つ風は1mしかありません。（2×cos60°＝１）
ですからこの場合，ヨットは1×3で3mゴールへ近づくことになります。
このときb→という風は，a→の方向に3m分の仕事をしたことになりますね。
この「3m」という数値こそがa→とb→の内積なのです。
もし風速2mの風がゴール方向へ吹いていたらなす角0°ですから，内積は 2×cos0°×3より「６」。つまりこの風はヨットに対して最大限の仕事をしてくれたことになります。
ゴール方向に対して垂直に吹いていたら，この風はゴールに進むために何の役にも立たないですよね。
このことは内積にもきちんと現れてきます。
なす角が90°ですから，内積は 2×cos90°×3より「０」。
「垂直ならば内積が0」というのはよく問題演習でも使う事実ですが，片方のベクトルがもう片方のベクトルのために何の仕事もしていないことを意味しているのです。
なす角が120°の状態で風が吹いたらどうでしょう。内積は 2×cos120°×3より「-3」ということになります。これは，この風がゴールへ進むのを「邪魔している」ことを意味します。だから，負の数が出てくるわけです。
内積の公式a→・b→=|a→| |b→|cosθの右辺は，|a→|×|b→|cosθと分解して読むとよいでしょうね。
|b→|cosθという部分で，風b→が，a→の方向にどれだけの影響を与えるかを計算していたのです。